4.7.4. Dihedral angles analysis — MDAnalysis.analysis.dihedrals¶
- Author
Henry Mull
- Year
2018
- Copyright
GNU Public License v2
New in version 0.19.0.
This module contains classes for calculating dihedral angles for a given set of atoms or residues. This can be done for selected frames or whole trajectories.
A list of time steps that contain angles of interest is generated and can be
easily plotted if desired. For the Ramachandran
and Janin classes, basic plots can be
generated using the method Ramachandran.plot() or Janin.plot().
These plots are best used as references, but they also allow for user customization.
See also
MDAnalysis.lib.distances.calc_dihedrals()function to calculate dihedral angles from atom positions
4.7.4.1. Example applications¶
4.7.4.1.1. General dihedral analysis¶
The Dihedral class is useful for calculating
angles for many dihedrals of interest. For example, we can find the phi angles
for residues 5-10 of adenylate kinase (AdK). The trajectory is included within
the test data files:
import MDAnalysis as mda
from MDAnalysisTests.datafiles import GRO, XTC
u = mda.Universe(GRO, XTC)
# selection of atomgroups
ags = [res.phi_selection() for res in u.residues[4:9]]
from MDAnalysis.analysis.dihedrals import Dihedral
R = Dihedral(ags).run()
The angles can then be accessed with Dihedral.angles.
4.7.4.1.2. Ramachandran analysis¶
The Ramachandran class allows for the
quick calculation of phi and psi angles. Unlike the Dihedral
class which takes a list of atomgroups, this class only needs a list of
residues or atoms from those residues. The previous example can repeated with:
u = mda.Universe(GRO, XTC)
r = u.select_atoms("resid 5-10")
R = Ramachandran(r).run()
Then it can be plotted using the built-in plotting method Ramachandran.plot():
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=plt.figaspect(1))
R.plot(ax=ax, color='k', marker='s')
as shown in the example Ramachandran plot figure.
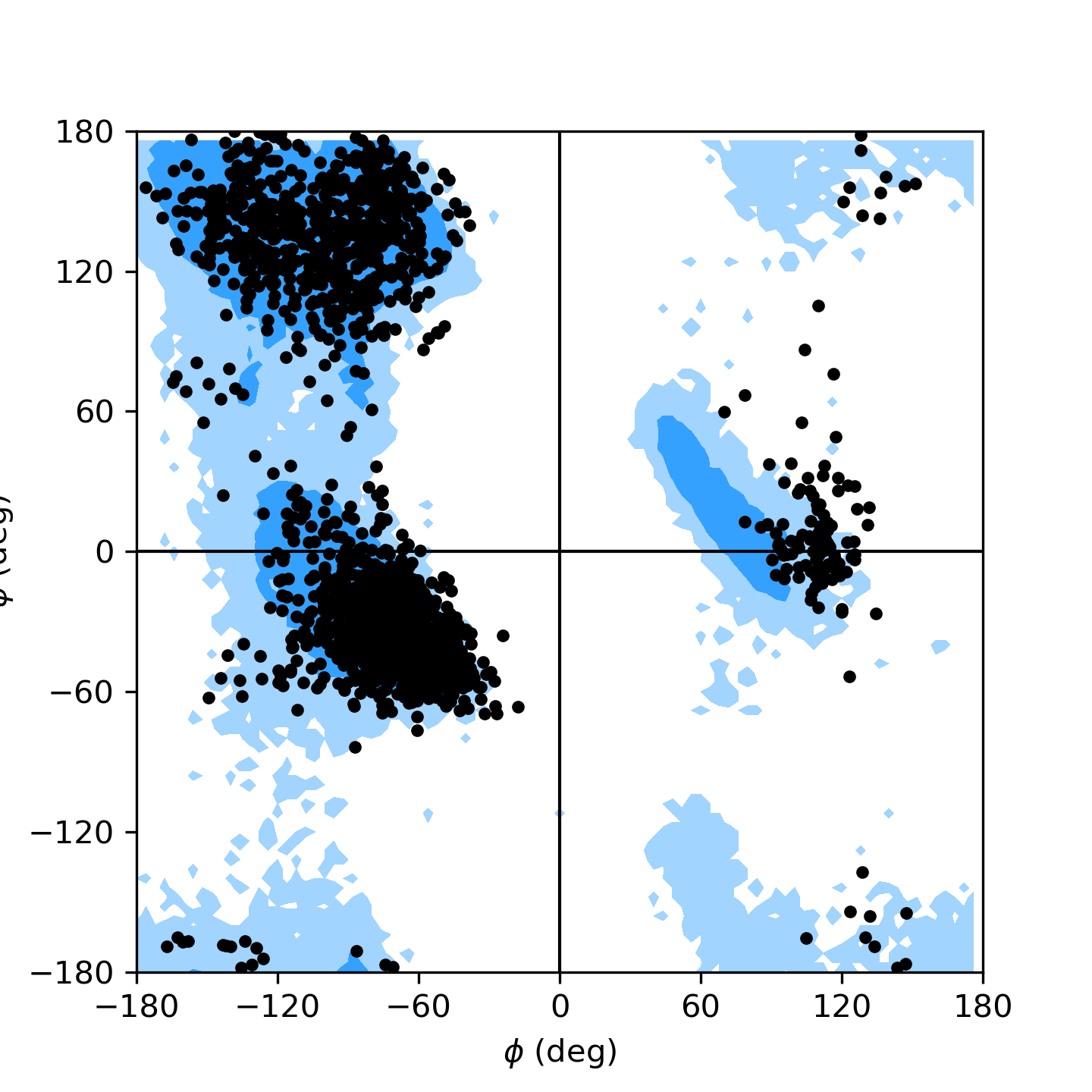
Ramachandran plot for residues 5 to 10 of AdK, sampled from the AdK test trajectory (XTC). The contours in the background are the “allowed region” and the “marginally allowed” regions.¶
The Janin class works in the same way, only needing a list of residues; see the
Janin plot figure as an example. To plot the data
yourself, the angles can be accessed using Ramachandran.angles or
Janin.angles.
Reference plots can be added to the axes for both the Ramachandran and Janin
classes using the kwarg ref=True. The Ramachandran reference data
(Rama_ref) and Janin reference data
(Janin_ref) were made using data
obtained from a large selection of 500 PDB files, and were analyzed using these
classes. The allowed and marginally allowed regions of the Ramachandran reference
plt have cutoffs set to include 90% and 99% of the data points, and the Janin
reference plot has cutoffs for 90% and 98% of the data points. The list of PDB
files used for the referece plots was taken from [Lovell2003] and information
about general Janin regions was taken from [Janin1978].
Note
These classes are prone to errors if the topology contains duplicate or missing
atoms (e.g. atoms with altloc or incomplete residues). If the topology has as
an altloc attribute, you must specify only one altloc for the atoms with
more than one ("protein and not altloc B").
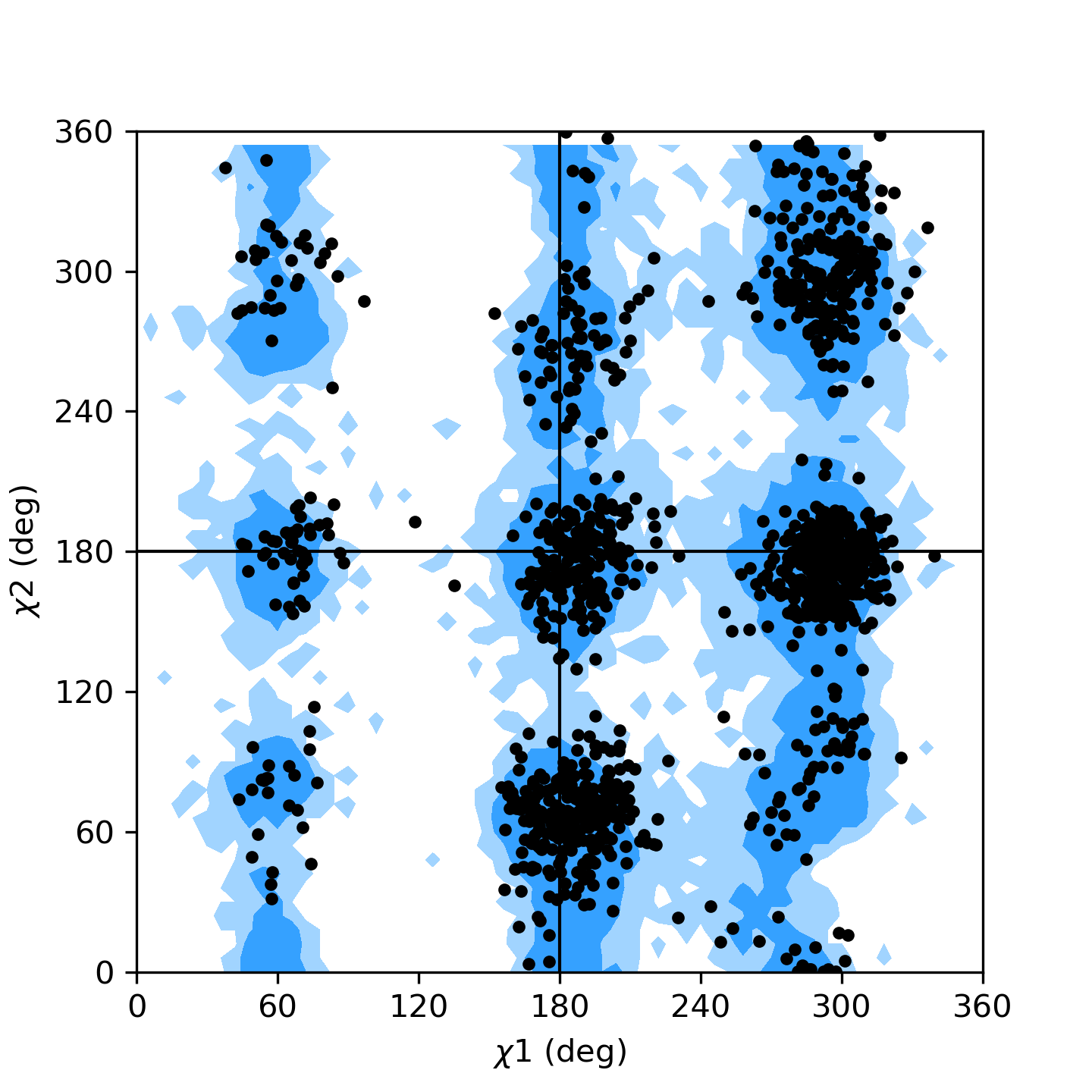
Janin plot for residues 5 to 10 of AdK, sampled from the AdK test trajectory (XTC). The contours in the background are the “allowed region” and the “marginally allowed” regions for all possible residues.¶
4.7.4.2. Analysis Classes¶
-
class
MDAnalysis.analysis.dihedrals.Dihedral(atomgroups, **kwargs)[source]¶ Calculate dihedral angles for specified atomgroups.
Dihedral angles will be calculated for each atomgroup that is given for each step in the trajectory. Each
AtomGroupmust contain 4 atoms.Note
This class takes a list as an input and is most useful for a large selection of atomgroups. If there is only one atomgroup of interest, then it must be given as a list of one atomgroup.
- Parameters
atomgroups (list) – a list of atomgroups for which the dihedral angles are calculated
- Raises
ValueError – If any atomgroups do not contain 4 atoms
-
angles¶ Contains the time steps of the angles for each atomgroup in the list as an
n_frames×len(atomgroups)numpy.ndarraywith content[[angle 1, angle 2, ...], [time step 2], ...].
-
run(start=None, stop=None, step=None, verbose=None)¶ Perform the calculation
-
class
MDAnalysis.analysis.dihedrals.Ramachandran(atomgroup, **kwargs)[source]¶ Calculate \(\phi\) and \(\psi\) dihedral angles of selected residues.
\(\phi\) and \(\psi\) angles will be calculated for each residue corresponding to atomgroup for each time step in the trajectory. A
ResidueGroupis generated from atomgroup which is compared to the protein to determine if it is a legitimate selection.Note
If the residue selection is beyond the scope of the protein, then an error will be raised. If the residue selection includes the first or last residue, then a warning will be raised and they will be removed from the list of residues, but the analysis will still run. If a \(\phi\) or \(\psi\) selection cannot be made, that residue will be removed from the analysis.
- Parameters
atomgroup (AtomGroup or ResidueGroup) – atoms for residues for which \(\phi\) and \(\psi\) are calculated
- Raises
ValueError – If the selection of residues is not contained within the protein
-
angles¶ Contains the time steps of the \(\phi\) and \(\psi\) angles for each residue as an
n_frames×n_residues×2numpy.ndarraywith content[[[phi, psi], [residue 2], ...], [time step 2], ...].
-
plot(ax=None, ref=False, **kwargs)[source]¶ Plots data into standard ramachandran plot. Each time step in
Ramachandran.anglesis plotted onto the same graph.- Parameters
ax (
matplotlib.axes.Axes) – If no ax is supplied or set toNonethen the plot will be added to the current active axes.ref (bool, optional) – Adds a general Ramachandran plot which shows allowed and marginally allowed regions
- Returns
ax – Axes with the plot, either ax or the current axes.
- Return type
-
run(start=None, stop=None, step=None, verbose=None)¶ Perform the calculation
-
class
MDAnalysis.analysis.dihedrals.Janin(atomgroup, **kwargs)[source]¶ Calculate \(\chi_1\) and \(\chi_2\) dihedral angles of selected residues.
\(\chi_1\) and \(\chi_2\) angles will be calculated for each residue corresponding to atomgroup for each time step in the trajectory. A
ResidueGroupis generated from atomgroup which is compared to the protein to determine if it is a legitimate selection.Note
If the residue selection is beyond the scope of the protein, then an error will be raised. If the residue selection includes the residues ALA, CYS, GLY, PRO, SER, THR, or VAL, then a warning will be raised and they will be removed from the list of residues, but the analysis will still run. Some topologies have altloc attribues which can add duplicate atoms to the selection and must be removed.
- Parameters
atomgroup (AtomGroup or ResidueGroup) – atoms for residues for which \(\chi_1\) and \(\chi_2\) are calculated
- Raises
ValueError – If the selection of residues is not contained within the protein
ValueError – If not enough or too many atoms are found for a residue in the selection, usually due to missing atoms or alternative locations
-
angles¶ Contains the time steps of the \(\chi_1\) and \(\chi_2\) angles for each residue as an
n_frames×n_residues×2numpy.ndarraywith content[[[chi1, chi2], [residue 2], ...], [time step 2], ...].
-
plot(ax=None, ref=False, **kwargs)[source]¶ Plots data into standard Janin plot. Each time step in
Janin.anglesis plotted onto the same graph.- Parameters
ax (
matplotlib.axes.Axes) – If no ax is supplied or set toNonethen the plot will be added to the current active axes.ref (bool, optional) – Adds a general Janin plot which shows allowed and marginally allowed regions
- Returns
ax – Axes with the plot, either ax or the current axes.
- Return type
-
run(start=None, stop=None, step=None, verbose=None)¶ Perform the calculation
References
- Lovell2003
Simon C. Lovell, Ian W. Davis, W. Bryan Arendall III, Paul I. W. de Bakker, J. Michael Word, Michael G. Prisant, Jane S. Richardson, and David C. Richardson (2003). “Structure validation by \(C_{\alpha}\) geometry: \(\phi\), \(\psi\), and \(C_{\beta}\) deviation”. Proteins 50(3): 437-450. doi: 10.1002/prot.10286
- Janin1978
Joël Janin, Shoshanna Wodak, Michael Levitt, and Bernard Maigret. (1978). “Conformation of amino acid side-chains in proteins”. Journal of Molecular Biology 125(3): 357-386. doi: 10.1016/0022-2836(78)90408-4

